Mathematics
While he is often regarded as a designer of mechanical devices, Archimedes also made contributions to the field of mathematics. Plutarch wrote: "He placed his whole affection and ambition in those purer speculations where there can be no reference to the vulgar needs of life."
Archimedes used the method of exhaustion to approximate the value of pi.
Archimedes was able to use infinitesimals in a way that is similar to modern integral calculus. Through proof by contradiction (reductio ad absurdum), he could give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay. This technique is known as the method of exhaustion, and he employed it to approximate the value of π. InMeasurement of a Circlehe did this by drawing a larger regular hexagon outside a circle and a smaller regular hexagon inside the circle, and progressively doubling the number of sides of each regular polygon, calculating the length of a side of each polygon at each step. As the number of sides increases, it becomes a more accurate approximation of a circle. After four such steps, when the polygons had 96 sides each, he was able to determine that the value of π lay between 31⁄7 (approximately 3.1429) and 310⁄71(approximately 3.1408), consistent with its actual value of approximately 3.1416. He also proved that the area of a circle was equal to π multiplied by the square of the radius of the circle (πr2). In On the Sphere and Cylinder, Archimedes postulates that any magnitude when added to itself enough times will exceed any given magnitude. This is the Archimedean property of real numbers.
In Measurement of a Circle, Archimedes gives the value of the square root of 3 as lying between 265⁄153 (approximately 1.7320261) and 1351⁄780 (approximately 1.7320512). The actual value is approximately 1.7320508, making this a very accurate estimate. He introduced this result without offering any explanation of how he had obtained it. This aspect of the work of Archimedes caused John Wallis to remark that he was: "as it were of set purpose to have covered up the traces of his investigation as if he had grudged posterity the secret of his method of inquiry while he wished to extort from them assent to his results."
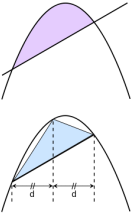
As proven by Archimedes, the area of the parabolic segment in the upper figure is equal to 4/3 that of the inscribed triangle in the lower figure.
In The Quadrature of the Parabola, Archimedes proved that the area enclosed by a parabola and a straight line is 4⁄3 times the area of a corresponding inscribed triangle as shown in the figure at right. He expressed the solution to the problem as an infinitegeometric series with the common ratio 1⁄4:
If the first term in this series is the area of the triangle, then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines, and so on. This proof uses a variation of the series 1/4 + 1/16 + 1/64 + 1/256 + · · · which sums to 1⁄3.
In The Sand Reckoner, Archimedes set out to calculate the number of grains of sand that the universe could contain. In doing so, he challenged the notion that the number of grains of sand was too large to be counted. He wrote: "There are some, King Gelo (Gelo II, son of Hiero II), who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited." To solve the problem, Archimedes devised a system of counting based on the myriad. The word is from the Greek μυριάς murias, for the number 10,000. He proposed a number system using powers of a myriad of myriads (100 million) and concluded that the number of grains of sand required to fill the universe would be 8 vigintillion, or 8×1063.
Archimedes used the method of exhaustion to approximate the value of pi.
Archimedes was able to use infinitesimals in a way that is similar to modern integral calculus. Through proof by contradiction (reductio ad absurdum), he could give answers to problems to an arbitrary degree of accuracy, while specifying the limits within which the answer lay. This technique is known as the method of exhaustion, and he employed it to approximate the value of π. InMeasurement of a Circlehe did this by drawing a larger regular hexagon outside a circle and a smaller regular hexagon inside the circle, and progressively doubling the number of sides of each regular polygon, calculating the length of a side of each polygon at each step. As the number of sides increases, it becomes a more accurate approximation of a circle. After four such steps, when the polygons had 96 sides each, he was able to determine that the value of π lay between 31⁄7 (approximately 3.1429) and 310⁄71(approximately 3.1408), consistent with its actual value of approximately 3.1416. He also proved that the area of a circle was equal to π multiplied by the square of the radius of the circle (πr2). In On the Sphere and Cylinder, Archimedes postulates that any magnitude when added to itself enough times will exceed any given magnitude. This is the Archimedean property of real numbers.
In Measurement of a Circle, Archimedes gives the value of the square root of 3 as lying between 265⁄153 (approximately 1.7320261) and 1351⁄780 (approximately 1.7320512). The actual value is approximately 1.7320508, making this a very accurate estimate. He introduced this result without offering any explanation of how he had obtained it. This aspect of the work of Archimedes caused John Wallis to remark that he was: "as it were of set purpose to have covered up the traces of his investigation as if he had grudged posterity the secret of his method of inquiry while he wished to extort from them assent to his results."
As proven by Archimedes, the area of the parabolic segment in the upper figure is equal to 4/3 that of the inscribed triangle in the lower figure.
In The Quadrature of the Parabola, Archimedes proved that the area enclosed by a parabola and a straight line is 4⁄3 times the area of a corresponding inscribed triangle as shown in the figure at right. He expressed the solution to the problem as an infinitegeometric series with the common ratio 1⁄4:
If the first term in this series is the area of the triangle, then the second is the sum of the areas of two triangles whose bases are the two smaller secant lines, and so on. This proof uses a variation of the series 1/4 + 1/16 + 1/64 + 1/256 + · · · which sums to 1⁄3.
In The Sand Reckoner, Archimedes set out to calculate the number of grains of sand that the universe could contain. In doing so, he challenged the notion that the number of grains of sand was too large to be counted. He wrote: "There are some, King Gelo (Gelo II, son of Hiero II), who think that the number of the sand is infinite in multitude; and I mean by the sand not only that which exists about Syracuse and the rest of Sicily but also that which is found in every region whether inhabited or uninhabited." To solve the problem, Archimedes devised a system of counting based on the myriad. The word is from the Greek μυριάς murias, for the number 10,000. He proposed a number system using powers of a myriad of myriads (100 million) and concluded that the number of grains of sand required to fill the universe would be 8 vigintillion, or 8×1063.
